GRAPH DAN TREE
-----------------------------
1. TEORI GRAF
Graf merupakan
gabungan dari himpunan simpul dan sisi yang dapat direpresentasikan dengan
gambar simpul yang dapat berupa titik dan dihubungkan oleh sisi berupa garis.
Berdasarkan definisi di atas dapat disimpulkan bahwa sebuah graf dapat
terbentuk dari himpunan simpul yang tidak boleh kosong dan himpunan sisi yang
boleh kosong.
Pada umumnya, graf digambarkan kumpulan simpul
dihubungkan oleh sisi yang merupakan suatu hubungan tertentu antar simpul yang
satu dan simpul yang lainnya.
Secara matemeatis, graf dapat didefinisikan sebagai
berikut.
Graf G = (V, E), yang dalam hal ini:
V = himpunan tidak-kosong dari simpul-simpul
(vertices)
= { v1 , v2 , ... , vn }
E = himpunan sisi (edges) yang menghubungkan sepasang
simpul
= {e1 , e2 , ... , en }
Berdasarkan ada tidaknya gelang atau sisi ganda pada
suatu graf, maka graf digolongkan menjadi dua jenis:
1.
Graf sederhana (simple graph).
Graf
yang tidak mengandung gelang maupun sisi- ganda dinamakan graf sederhana. G1
pada Gambar 2 adalah contoh graf sederhana.
2.
Graf tak-sederhana (unsimple-graph).
Graf
yang mengandung sisi ganda atau gelang dinamakan graf tak-sederhana (unsimple
graph).
G2
dan G3 pada Gambar 2 adalah contoh graf tak-sederhana.
Selain teori dasar graf di atas, terdapat terminologi-
terminologi dasar lainnya yang berkaitan dengan graf. Terminologi ini sangat
penting untuk memahami teori graf selanjutnya. Terminologi dasar tersebut
antara lain adalah sebagai berikut.
A.
Lintasan
Lintasan yang panjangnya n dari simpul awal v0 ke simpul
tujuan vn adalah barisan berselang-seling simpul- simpul dan sisi-sisi yang
berbentuk v0, e1, v1, e2, v2
,vn-1, en, vn sedemikian sehingga e1 = (v0, v1), e2 =
(v1, v2),… , en = (vn-1, vn) adalah sisi-sisi dari graf G. (Munir, 2012).
Sebuah lintasan dikatakan lintasan sederhana jika
semua simpulnya berbeda, yaitu setiap sisi yang dilalui hanya satu kali.
Lintasan tertutup adalah lintasan yang berawal dan berakhir pada simpul yang
sama.
Sebaliknya, lintasan terbuka adalah lintasan yang
berawal dan berakhir tidak pada simpul yang sama.
B.
Terhubung
Dua buah simpul u dan simpul v dikatakan terhubung
bila terdapat lintasan antara simpul u dan simpul v. Secara formal, graf
terhubung dapat didefinisikan sebagai berikut.
Graf tak-berarah G disebut graf terhubung jika untuk
setiap pasang simpul u dan v di dalam himpunan V terdapat lintasan dari u ke v.
Jika tidak, maka graf G disebut graf tidak terhubung. (Munir, 2012)
Graf yang hanya memiliki satu simpul saja, dikatakan
graf terhubung karena graf pada simpul itu, terhubung dengan dirinya sendiri.
C.
Upagraf Merentang
Upagraf G1 = (V1, E1) dari G = (V, E) dikatakan
upagraf merentang jika V1 = V dengan kata lain, G1 mengandung semua simpul G.
(Munir, 2012)
Bila terdapat satu buah simpul (vx) dengan vx adalah
simpul dari G tetapi vx bukan simpul dari G1, maka G1 bukanlah upagraf
merentang dari G. Untuk lebih jelasnya, upagraf merentang dapat dilihat pada
gambar di bawah ini.
D.
Graf Berbobot
Graf berbobot atau weighted graph adalah graf yang
setiap sisinya diberikan sebuah nilai atau harga. Harga atau nilai pada sisi
graf merupakan representasi dari masalah yang dimodelkan ke dalam graf. Nilai
tersebut dapat merepresentasikan biaya perjalanan, waktu tempuh pesan, ongkos
produksi, bahkan kompleksitas dari sebuah algoritma suatu program.
Graf berbobot merupakan istilah khusus dari graf
label. Pada graf berbobot, nilai hanya bisa diberikan pada setiap sisi graf
saja, namun pada graf label nilai bisa diberikan pula pada simpul graf.
Misalnya pada graf yang memodelkan kota-kota, simpul diberi label nama-nama
kota sedangkan sisi-sisi diberi label jarak antar kota.
Terminologi-terminologi dasar di atas sangat berguna
untuk memahami teori-teori pohon. Karena pada dasarnya pohon merupakan graf
juga. Selanjutnya akan dijelaskan tentang teori-teori pohon.
E.
Graf Berarah
Graf berarah adalah graf yang setiap sisinya memiliki
orientasi arah. Graf berarah dikatakan terhubung jika graf tidak berarahnya
terhubung. Dua simpul pada graf berarah disebut berhubung kuatapabila terdapat
lintasan berarah dari simpul yang satu ke simpul yang lain dan sebaliknya.
Apabila simpul hanya terhubung oleh satu sisi yang berarah maka disebut
terhubung lemah.
Terminologi pada graf diantaranya berikut ini.
1. Ketetanggaan (Adjacent)
Dua buah simpul dikatakan bertetangga bila keduanya
terhubung langsung.
2. Derajat (Degree)
Derajat suatu simpul adalah jumlah sisi yang
bersisian dengan simpul tersebut. Notasi: d(v)
3. Lintasan (Path)
Lintasan yang panjangnya n dari simpul awal v0 ke
simpul tujuan vn di dalam graf G ialah barisan berselang- seling simpul-simpul
dan sisi-sisi yang berbentuk v0, e1, v1, e2, v2,... , vn –1, en, vn sedemikian
sehingga e1 = (v0, v1), e2 = (v1, v2), ... , en = (vn-1, vn) adalah sisi-sisi
dari graf G.
4. Siklus (Cycle) atau Sirkuit (Circuit)
Lintasan yang berawal dan berakhir pada simpul yang
sama disebut sirkuit atau siklus.
Salah satu aplikasi graf yaitu Pohon. Pohon adalah
graf tak-berarah terhubung yang tidak mengandung sirkuit.
Contoh listing program
|
#include <iostream.h>
#include <conio.h> int main(){ bool ketemu,nolsemua; int matrix[10] [10]; int i,j,jumlah_simpul,jumlah_sisi,asal,tujuan; //isnisialisasi matrix cout<<"jumlah simpul:"; cin>>jumlah_simpul; cout<<"jumlah_sisi:"; cin>>jumlah_sisi; for (i=1;i<=jumlah_simpul;i++) for (j=1;j<=jumlah_simpul;j++) matrix[i][j]=0; //isi matrix sesuai input graf for (i=1;i<=jumlah_sisi;i++){ cout<<"simpul asal:"; cin>>asal; cout<<"simpul tujuan:"; cin>>tujuan; matrix[asal][tujuan]=1; matrix[tujuan][asal]=1; } //telusuri graf i=1;nolsemua=false; while (i<=jumlah_simpul && !nolsemua){ j=1;ketemu=false; while (j<=jumlah_simpul && !ketemu){ if (matrix[i][j]==1) ketemu=true; else j++; } if (!ketemu) nolsemua=true; else i++; } if(nolsemua) cout<<"graf tidak terhubung"; else cout<<"graf terhubung"; getch(); } |
2. TEORI POHON
Sementara itu, pengurutan data menggunakan metode Tree C++, memiliki beberapa istilah/cara yang berbeda. Yaitu:
Struktur Tree terdiri dari node bertingkat yang
mempunyai peran sesuai tingkatan masing-masing. Tingkatan itu adalah: Parent
(orang tua), Child (anak). Dalam program Tree C++, dikenal beberapa istilah
umum berikut ini:
1.
Predecessor: Node yang berada diatas Successor
atau sebuah node tertentu (Parent).
2.
Successor: Node yang berada dibawah Predecessor
atau node tertentu (Child).
3.
Parent: Predecessor diatas sebuah node atau
diatas Successor.
4.
Child: Successor dibawah sebuah node atau
dibawah Predecessor.
5.
Root (Akar): Node tanpa Predecessor yang berada
paling ujung atas.
6.
Leaf (Daun): Node tanpa Successor yang berada
paling ujung bawah.
7.
Sibling (Saudara Kandung): Node-node yang
mempunyai Parent yang sama.
Sementara itu, pengurutan data menggunakan metode Tree C++, memiliki beberapa istilah/cara yang berbeda. Yaitu:
1.
PreOrder : Cetak node - Kunjungi node kiri -
Kunjungi node kanan.
2.
InOrder : Kunjungi node kiri - Cetak node -
Kunjungi node kanan.
3.
PostOrder : Kunjungi node kiri - Kunjungi node
kanan - Cetak node.
Pohon adalah suatu graf yang tidak mengandung
lintasan sederhana. Oleh karena itu, pohon tidak mengandung sisi ganda
(multiple edge) maupun gelang (loop). Ada dua tipe pohon yaitu pohon tidak
berakar dan pohon berakar.
Pohon adalah suatu graf yang tidak mengandung
lintasan sederhana. Oleh karena itu, pohon tidak mengandung sisi ganda
(multiple edge) maupun gelang (loop). Ada dua
tipe pohon yaitu pohon tidak berakar dan pohon
berakar
A.
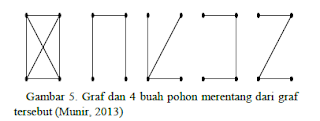
Pohon Merentang
Pohon merentang adalah pohon T yang semua simpulnya
sama dengan semua simpul pada graf G, dan sisi pada pohon T merupakan anggota
himpunan sisi pada graf G. Dengan kata lain, jika upagraf dari graf terhubung
berbentuk pohon, maka upagraf merentang tersebut dinamakan pohon merentang.
Pohon merentang minimum adalah pohon merentang dari
graf G yang bernilai paling minimum. Pohon merentang minimum merupakan bagian
terpenting dari makalah ini karena digunakan untuk menentukan jalur trem yang
paling efektif dan paling murah.
Untuk mencari pohon merentang minimum, dapat
dilakukan dengan menggunakan dua algoritma, yaitu algoritma Prim dan algortima
Kruskal.
B.
Algoritma Prim
Algoritma Prim (Munir, 2013)
1.
Ambil sisi dari graf G yang berbobot minimum,
masukkan ke dalam T.
2.
Pilih
sisi e yang mempunyai bobot minimum dan bersisian dengan simpul di T, tetapi e
tidak membentuk sirkuit di T. Masukkan e ke dalam T.
3.
Ulangi 2 sebanyak n – 2 kali.
B.
Algoritma Kruskal
1.
T masih kosong.
2.
Pilih sisi e dengan bobot yang minimum yang
tidak membentuk sirkuit di T. Masukkan e ke dalam T.
3.
Ulangi langkah 2 sebanyak n – 2.
Contoh program Kruskal:
|
/header file
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
//pendeklarasian struct sebuah tree awal
struct Node{
int data;
Node *kiri;
Node *kanan;
};
//fungsi untuk menambahkan node baru
void tambah(Node **root, int databaru)
{
//jika root masih
kosong
if((*root) == NULL)
{
//pembuatan node baru
Node *baru;
//pengalokasian memori dari node yang telah dibuat
baru = new Node;
//inisialisasi awal node yang baru dibuat
baru->data = databaru;
baru->kiri = NULL;
baru->kanan = NULL;
(*root) = baru;
(*root)->kiri = NULL;
(*root)->kanan = NULL;
printf("Data bertambah!");
}
//jika data yang akan
dimasukkan lebih kecil daripada elemen root, maka akan diletakkan di node
sebelah kiri.
else if(databaru<(*root)->data)
tambah(&(*root)->kiri, databaru);
//jika data yang akan
dimasukkan lebih besar daripada elemen root, maka akan diletakkan di node
sebelah kanan
else if(databaru>(*root)->data)
tambah(&(*root)->kanan, databaru);
//jika saat dicek data
yang akan dimasukkan memiliki nilai yang sama dengan data pada root
else if(databaru ==
(*root)->data)
printf("Data sudah ada!");
}
//fungsi yang digunakan untuk mencetak tree secara
preOrder
void preOrder(Node *root)
{
if(root != NULL){
printf("%d ", root->data);
preOrder(root->kiri);
preOrder(root->kanan);
}
}
//fungsi yang digunakan untuk mencetak tree secara
inOrder
void inOrder(Node *root)
{
if(root != NULL){
inOrder(root->kiri);
printf("%d ", root->data);
inOrder(root->kanan);
}
}
//fungsi yang digunakan untuk mencetak tree secara
postOrder
void postOrder(Node *root)
{
if(root != NULL){
postOrder(root->kiri);
postOrder(root->kanan);
printf("%d ", root->data);
}
}
//fungsi utama
int main()
{
//deklarasikan
variabel
int pil, data;// c;
Node *pohon; //*t;
pohon = NULL; //inisialisasi
node pohon
//perulangan
do-while
do
{
system("cls"); //bersihkan layar
printf("\t#PROGRAM TREE C++#");
printf("\n\t==================");
printf("\nMENU");
printf("\n----\n");
printf("1. Tambah\n");
printf("2. Lihat pre-order\n");
printf("3. Lihat in-order\n");
printf("4. Lihat post-order\n");
printf("5. Exit\n");
printf("Pilihan : ");
scanf("%d", &pil);
switch(pil)
{
//jika pil bernilai 1
case 1 :
printf("\nINPUT : ");
printf("\n-------");
printf("\nData baru : ");
scanf("%d", &data);
//panggil fungsi untuk menambah node yang berisi data pada tree
tambah(&pohon, data);
break;
//jika pil bernilai 2
case 2 :
printf("\nOUTPUT PRE ORDER : ");
printf("\n------------------\n");
if(pohon!=NULL)
//panggil fungsi untuk mencetak data secara preOrder
preOrder(pohon);
else
printf("Masih kosong!");
break;
//jika pil bernilai 3
case 3 :
printf("\nOUTPUT IN ORDER : ");
printf("\n------------------\n");
if(pohon!=NULL)
//panggil fungsi untuk mencetak data secara inOrder
inOrder(pohon);
else
printf("Masih kosong!");
break;
//jika pil bernilai 4
case 4 :
printf("\nOUTPUT POST ORDER : ");
printf("\n------------------\n");
if(pohon!=NULL)
//panggil fungsi untuk mencetak data secara postOrder
postOrder(pohon);
else
printf("Masih kosong!");
break;
}
_getch();
}while(pil != 5); //akan
diulang jika input tidak samadengan 5
return EXIT_FAILURE;
}
|





Tidak ada komentar:
Posting Komentar