SORTING
(PENGURUTAN)
Pengurutan data dalam
struktur data sangat penting terutama untuk data yang bertipe data numerik
ataupun karakter. Pengurutan dapat dilakukan secara ascending (urut naik) dan descending
(urut turun). Pengurutan (Sorting)
adalah proses pengurutan data yang sebelumnya disusun secara acak sehingga
tersusun secara teratur menurut aturan tertentu.
Contoh ;
Data Acak : 3 9 6 21 10 1 13
Ascending : 1 3 6 9 10 13 21
Descending : 21 13
10 9 6 3 1
Deklarasi Array Sorting
Mendeklarasikan array secara global :
Int data[100];
Int n;//untuk jumlah data
|
Fungsi tukar 2 buah data :
Void tukar (int a, int b)
{
int tmp;
tmp= data[a];
data[a] = data [b];
data [b] = tmp;
}
|
Beberapa Algoritma untuk melakuka sorting :
1. Buble sort
Merupakan metode sorting
termudah, diberi nama “Bubble” karena proses pengurutan secara berangsur-angsur
bergerak/berpindah ke posisinya yang tepat, seperti gelembung yang keluar dari
sebuah gelas bersoda. Bubble Sortmengurutkan data dengan cara membandingkan
elemen sekarang dengan elemen berikutnya. Jika elemen sekarang lebih besar dari
elemen berikutnya maka kedua elemen tersebut ditukar, jika pengurutan ascending. Jika elemen sekarang lebih
kecil dari elemen berikutnya, maka kedua elemen tersebut ditukar, jika
pengurutan descending. Algoritma ini
seolah-olah menggeser satu per satu elemen dari kanan ke kiri atau kiri ke
kanan, tergantung jenis pengurutannya. Ketika satu proses telah selesai, maka
bubble sort akan mengulangi proses, demikian seterusnya. Kapan berhentinya?
Bubble sort berhenti jika seluruh array telah diperiksa dan tidak ada
pertukaran lagi yang bisa dilakukan, serta tercapai perurutan yang telah
diinginkan.
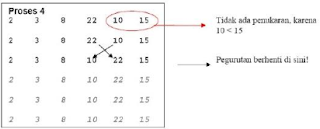
Pada gambar diatas, pengecekan dimulai dari data yang
paling akhir , kemudian dibandingkan dengan data didepannya, jika data
didepannya lebih besar maka akan ditukar.
Pada proses ke-2, pengecekan dilakukan sampai dengan
data ke-2 karena data pertama pasting sudah paling kecil.
Sintaks program fungsi buble sort
:
void bubble sort ()
{
for (int i = 1; i<n;
i++)
{
for (int j = n-1; j>=1; j--)
{
if (data [j]< data [j-1])
tukar (j, j-1); // ascending
}
}
|
Dengan
prosedur diatas, data terurut naik (ascending),
untuk urut turun (descending)
silahkan ubah bagian :
If (data [j] <data [j-1])
Menjadi :
If (data [j] > data
[j-1])
Tukar (j, j-1);
Algoritma buble sorting mudah dalam sintaks, tetapi lebh hemat dibandingkan
algoritma sorting yang lain.
2. Quick sort
Algoritma quick
sort sangat sederhana dalam teori, tetapi sangat sulit untuk diterjemahkan
ke dalam sebuah code karena pengurutan dilakukan dalam sebuah list dan diproses
secara rekursif. Algoritma ini terdisi dari empat langkah (yang mana menyerupai
merge sort) yaitu :
· Memilih
sebuah elemen untuk dijadikan poros atau pivot point (biasanya elemen
· paling
kiri dari tabel).
· Membagi
tabel menjadi dua bagian, satu dengan elemen yang lebih besar dari poros, dan
satu lagi untuk elemen yang lebih kecil dari poros.
· Mengulang
algoritma untuk kedua buah tabel secara rekursif.
Tingkat keefektifan dari algoritma ini dangat bergantung
pada elemen yang dipilih menjadi poros. Kasus terburuk terjadi ketika tabel
sudah terurut dan elemen terkecil di sebelah kiri menjadi poros. Kasus ini
mempunyai kompleksitas algoritma O(n2). Maka dari itu sangat
disarankan untuk memilih poros bukan dari elemen paling kiri dari tabel, tetapi
dipilih secara random. Selama poros dipilih secara random, algoritma quick sort mempunyai kompleksitas
algoritma sebesar O (n log n).
Contoh program :
void quickSort(int T[], int
Nmax)
/*I.S. T tabel dgn elemen
bertipe*/
/* integer, sembarang*/
/*F.S. T terurut menaik*/
/*Proses : melakukan
pengurutan*/
/* dengan metode quick sort*/
{
q_sort(T, 0, Nmax - 1);
}
void q_sort(int T[], int left,
int
right)
{
int pivot, l_hold, r_hold;
l_hold = left;
r_hold = right;
pivot = T[left];
while (left < right)
{
while ((T[right] >=
pivot) &&
(left < right))
right--;
if (left != right)
{
T[left] = T[right];
left++;
}
while ((T[left] <=
pivot) && (left
< right))
left++;
if (left != right)
{
T[right] = T[left];
right--;
}
}
T[left] = pivot;
pivot = left;
left = l_hold;
right = r_hold;
if (left < pivot)
q_sort(T, left, pivot-1);
if (right > pivot)
q_sort(T, pivot+1, right);
}
|
Algoritma quick
sort mengurutkan dengan sangat cepat, namun algoritma ini sangat komplex
dan diproses secara rekursif. Sangat memungkinkan untuk menulis algoritma yang lebih
cepat untuk beberapa kasus khusus, namun untuk kasus umum, sampai saat ini
tidak ada yang lebih cepat dibandingkan algoritma quick sort. Walaupun begitu algoritma quick sort tidak selalu merupakan pilihan yang terbaik. Seperti yang
telah disebutkan sebelumnya, algoritma ini dilakukan secara rekursif yang
berarti jika dilakukan untuk tabel yang berukuran sangat besar, walaupun cepat,
dapat menghabiskan memori yang besar pula. Selain itu, algoritma ini adalah
algoritma yang terlalu komplex untuk mengurutkan tabel yang berukuran kecil
(hanya puluhan elemen misalnya). Selain itu algoritma quick sort mempunyai tingkat efisiensi yang buruk ketika
dioperasikan pada tabel yang hampir terurut atau pada tabel yang terurut menurun.
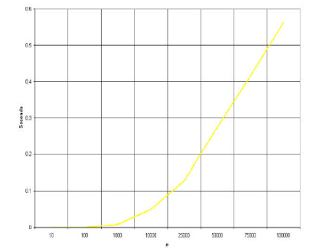
Grafik di atas
menggambarkan kompleksitas algoritma dari quick
sort.
3. Marge sort
Algoritma merge sort membagi (split) table menjadi dua
tabel sama besar. Masing-masing tabel diurutkan secara rekursif, dan kemudian digabungkan
kembali untuk membentuk table yang terurut. Implementasi dasar dari algoritma merge
sort memakai tiga buah tabel, dua untuk menyimpan elemen dari tabel yang telah
dibagi dua dan satu untuk menyimpan elemen yang telah teurut. Namun algoritma ini dapat juga dilakukan langsung
pada dua tabel, sehingga menghemat
ruang atau memori yang dibutuhkan. Di bawah ini adalah
algoritma untuk marge sort yang dilakukan pada dua tabel.
Contoh program Marge sort:
void mergeSort(int *T, int *temp, int
Nmax)
/*I.S. T tabel dgn elemen bertipe*/
/* integer, T tidak kosong*/
/*F.S. T terurut menaik*/
/*Proses : melakukan pengurutan*/
/* dengan metode merge sort*/
{
m_sort(T, temp, 0, Nmax - 1);
}
void m_sort(int *T, int *temp, int
*left, int *right)
{
int mid;
if (*right > *left)
{
mid = (*right + *left) / 2;
m_sort(T, temp, left, mid);
m_sort(T, temp, mid+1, right);
merge(T, temp, left, mid+1,
right);
}
}
void merge(int *T, int *temp, int
left, int mid, int right)
{
int i, left_end, num_elements,
tmp_pos;
left_end = mid - 1;
tmp_pos = left;
num_elements = right - left + 1;
while ((left <= left_end) && (mid <=
right))
{
if (*T[left] <= *T[mid])
{
*temp[tmp_pos] = *T[left];
tmp_pos = tmp_pos + 1;
left = left +1;
}
else
{
*temp[tmp_pos] =* T[mid];
tmp_pos = tmp_pos + 1;
mid = mid + 1;
}
}
while (left <= left_end)
{
*temp[tmp_pos] = *T[left];
left = left + 1;
tmp_pos = tmp_pos + 1;
}
while (mid <= right)
{
*temp[tmp_pos] = *T[mid];
mid = mid + 1;
tmp_pos = tmp_pos + 1;
}
for (i=0; i <= num_elements; i++)
{
*T[right] = *temp[right];
right = right - 1;
}
}
|
Karena algoritma marge sort adalah
algoritma yang dijalankan secara rekursif maka T(n) dari algoritma ini adalah :
Sehingga, algoritma merge sort memiliki kompleksitas
algoritma O(n log n).
Algoritma merge sort ini sebenernya lebih
cepat dibandingkan heap sort untuk tabel yang lebih besar. Namun, algoritma ini
membutuhkan setidaknya ruang atau emori dua kali lebih besar karena dilakukan
secara rekursif dan memakai dua tabel. Hal ini menyebabkan algoritma ini kurang
banyak dipakai.
Grafik di atas menggambarkan kompleksitas algoritma
dari marge sort.
Sumber :








Tidak ada komentar:
Posting Komentar